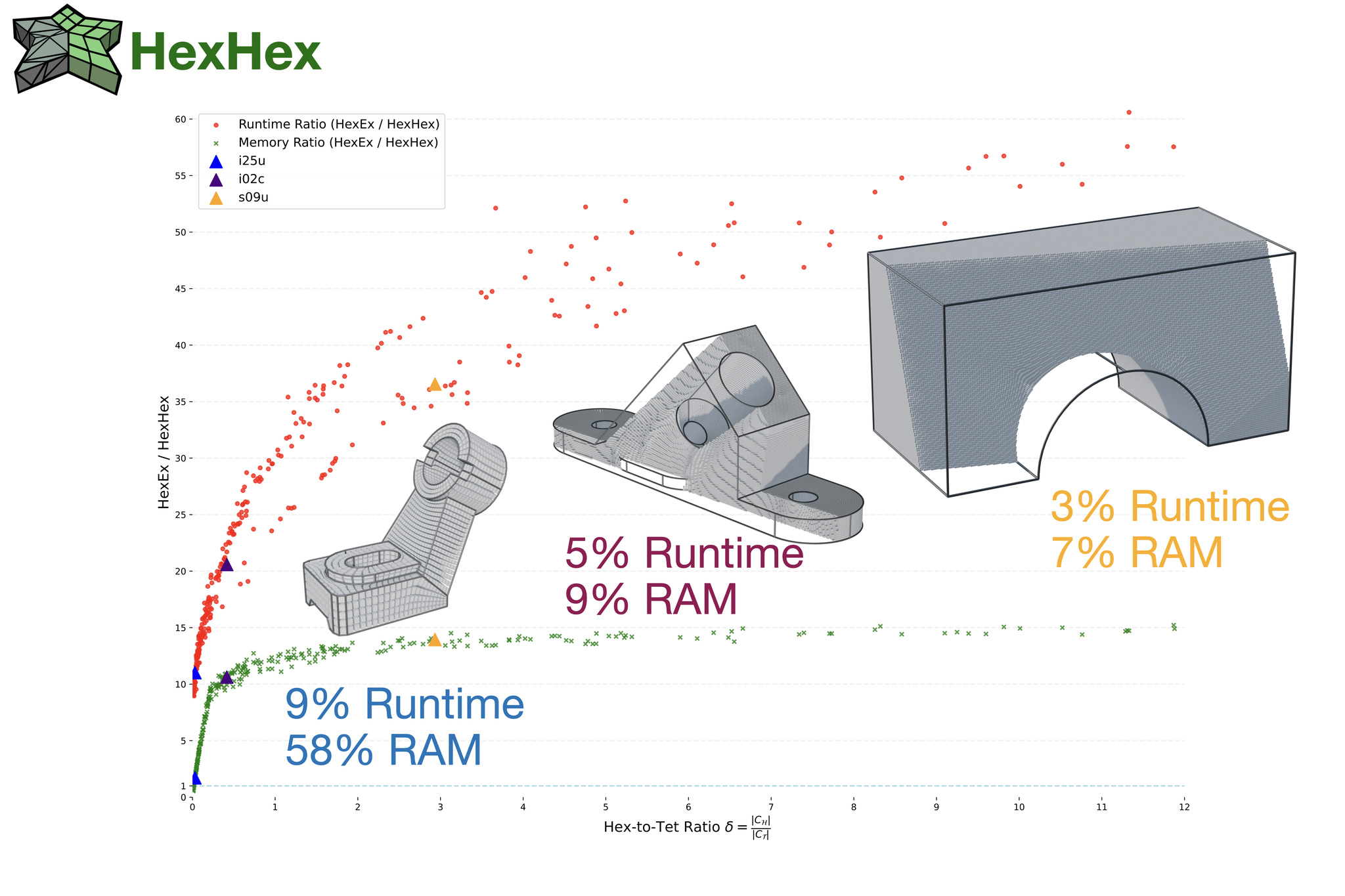
Modern hexahedral mesh generation relies on integer-grid maps (IGM), which map the Cartesian grid of integer iso-surfaces to a structure-aligned and conforming hexahedral cell complex discretizing the target shape. The hexahedral mesh is formed by iso-surfaces of the map such that an extraction algorithm is needed to convert the implicit map representation into an explicit mesh. State-of-the-art algorithms have been designed with two goals in mind, i.e., (i) unconditional robustness and (ii) tolerance to map defects in the form of inverted or degenerate tetrahedra. Because of significant advancements in the generation of locally injective maps, the tolerance to map defects has become irrelevant. At the same time, there is a growing demand for efficiently handling significantly larger mesh complexities, unfortunately not well served by the state-of-the-art since the tolerance to map defects induces a high runtime cost. Consequently, we present HexHex, a novel (unconditionally robust) hexahedral mesh extraction algorithm for locally injective integer-grid maps designed for maximal performance and scalability. Key contributions include a novel and highly compact mesh data structure based on so-called propellers and a conservative rasterization technique, significantly reducing the number of required exact predicate tests. HexHex not only offers lower asymptotic runtime complexities from a theoretical perspective but also lower constants, enabling in practice a 30x speedup for medium-sized examples and a larger speedup for more complex inputs, specifically when the hex-to-tet ratio is large. We provide a C++ reference implementation, supporting multi-core parallelization and the extraction of curved (piecewise-linear) hexahedral mesh edges and faces, e.g., valuable for subsequent higher-order mesh generation.
