 Expansion Cones: A Progressive Volumetric Mapping Framework
Expansion Cones: A Progressive Volumetric Mapping Framework
SIGGRAPH 2023 Volumetric mapping is a ubiquitous and difficult problem in Geometry Processing and has been the subject of research in numerous and various directions. While several methods show encouraging results, the field still lacks a general approach with guarantees regarding map bijectivity. Through this work, we aim at opening the door to a new family of methods by providing a novel framework based on the concept of progressive expansion. Starting from an initial map of a tetrahedral mesh whose image may contain degeneracies but no inversions, we incrementally adjust vertex images to expand degenerate elements. By restricting movement to so-called expansion cones, it is done in such a way that the number of degenerate elements decreases in a strictly monotonic manner, without ever introducing any inversion. Adaptive local refinement of the mesh is performed to facilitate this process. We describe a prototype algorithm in the realm of this framework for the computation of maps from ball-topology tetrahedral meshes to convex or star-shaped domains. This algorithm is evaluated and compared to state-of-the-art methods, demonstrating its benefits in terms of bijectivity. We also discuss the associated cost in terms of sometimes significant mesh refinement to obtain the necessary degrees of freedom required for establishing a valid mapping. Our conclusions include that while this algorithm is only of limited immediate practical utility due to efficiency concerns, the general framework has the potential to inspire a range of novel methods improving on the efficiency aspect.

|
|
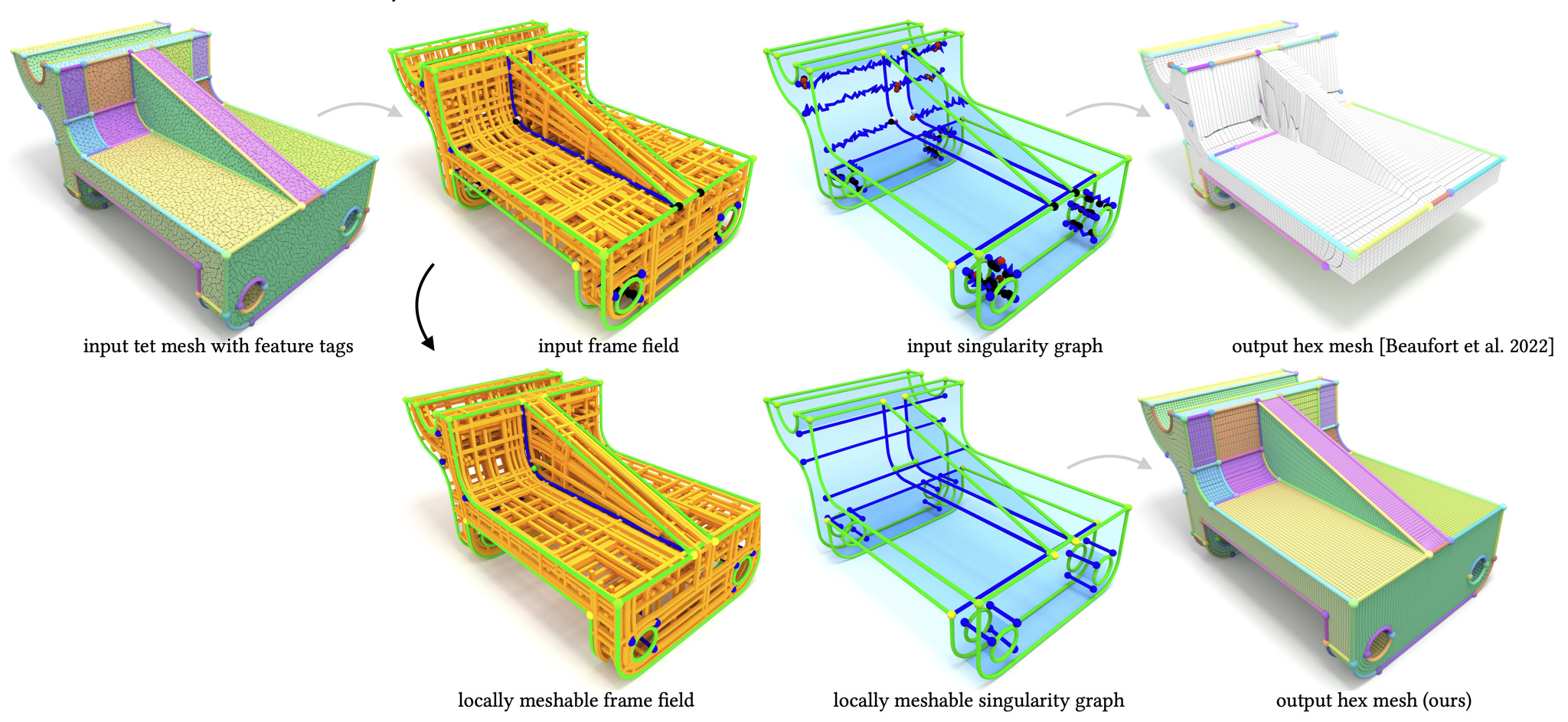 Locally Meshable Frame Fields
Locally Meshable Frame Fields
SIGGRAPH 2023 The main robustness issue of state-of-the-art frame field based hexahedral mesh generation algorithms originates from non-meshable topological configurations, which do not admit the construction of an integer-grid map but frequently occur in smooth frame fields. In this article, we investigate the topology of frame fields and derive conditions on their meshability, which are the basis for a novel algorithm to automatically turn a given non-meshable frame field into a similar but locally meshable one. Despite local meshability is only a necessary but not sufficient condition for the stronger requirement of meshability, our algorithm increases the 2% success rate of generating valid integer-grid maps with state-of-the-art methods to 58%, when compared on the challenging HexMe dataset.

|
|
 Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization
Min-Deviation-Flow in Bi-directed Graphs for T-Mesh Quantization
SIGGRAPH 2023 Subdividing non-conforming T-mesh layouts into conforming quadrangular meshes is a core component of state-of-the-art (re-)meshing methods. Typically, the required constrained assignment of integer lengths to T-Mesh edges is left to generic branch-and-cut solvers, greedy heuristics, or a combination of the two. This either does not scale well with input complexity or delivers suboptimal result quality. We introduce the Minimum-Deviation-Flow Problem in bi-directed networks (Bi-MDF) and demonstrate its use in modeling and efficiently solving a variety of T-Mesh quantization problems. We develop a fast approximate solver as well as an iterative refinement algorithm based on graph matching that solves Bi-MDF exactly. Compared to the state-of-the-art QuadWild implementation on the authors' 300 dataset, our exact solver finishes after only 0.49% (total 17.06s) of their runtime (3491s) and achieves 11% lower energy while an approximation is computed after 0.09% (3.19s) of their runtime at the cost of 24% increased energy. A novel half-arc-based T-Mesh quantization formulation extends the feasible solution space to include previously unattainable quad meshes. The Bi-MDF problem is more general than our application in layout quantization, potentially enabling similar speedups for other optimization problems that fit into the scheme, such as quad mesh refinement.

|







