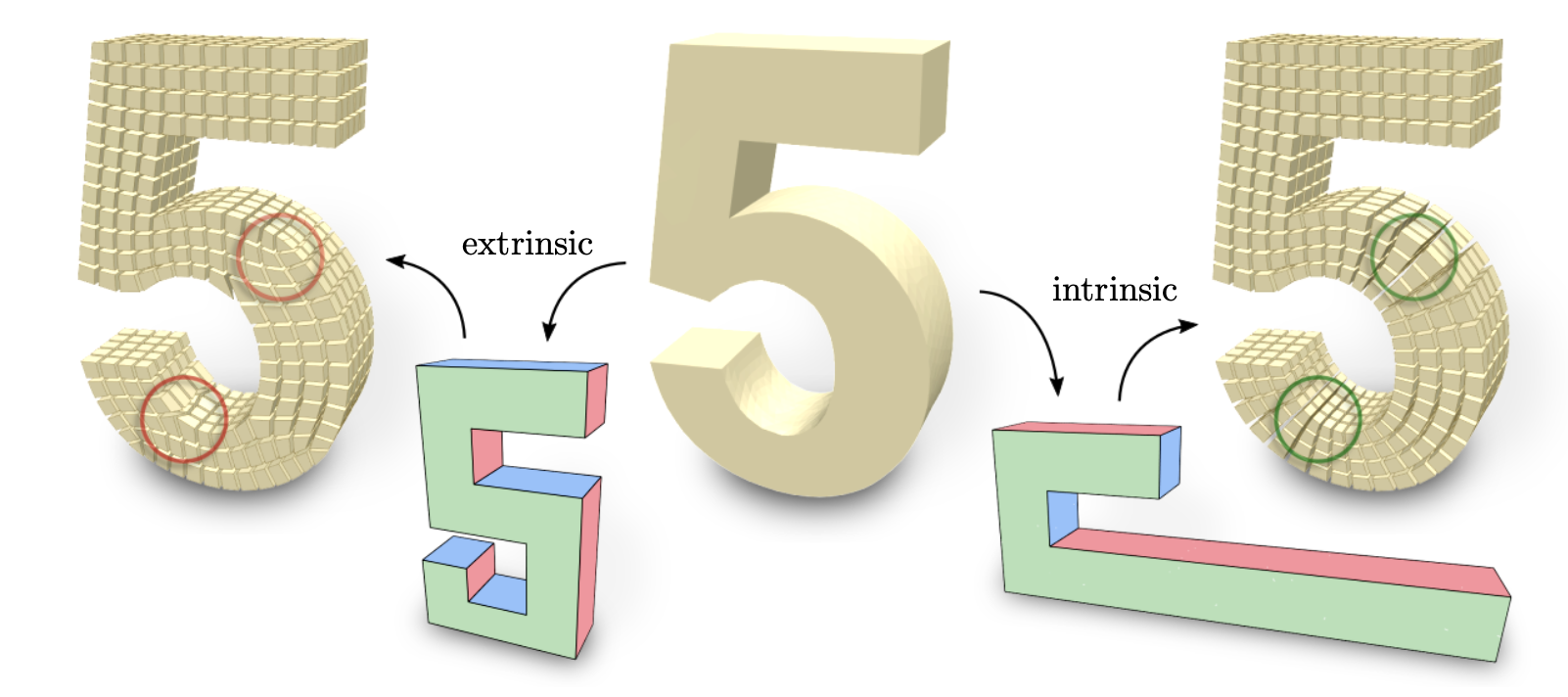
Polycube mapping is an attractive approach for the generation of all-hexahedral meshes with a fully regular interior, i.e. free of internal singular edges or vertices. It is based on determining a low distortion map between the input model and a polycube domain, which then pulls back the regular voxel grid to form a hexahedral mesh for the model. Automatically finding an appropriate polycube domain for a given model, however, is a challenging problem. Existing algorithms are either very sensitive to the embedding and orientation of the input model, restricted to only subclasses of possible domains, or depend crucially on some initialization because they rely on a non-convex optimization formulation. This can easily lead to unsatisfactory and unnecessary corners and edges in the polycube structure. We present a novel approach to the problem of finding high-quality polycube domains. It is based on an entirely intrinsic formulation as a mixed integer optimization problem, which can be tackled by solving a series of simple convex problems, each of which can be solved to the global optimum. Experiments demonstrate that our method avoids many of the undesired corners and surface irregularities common to many previous methods.