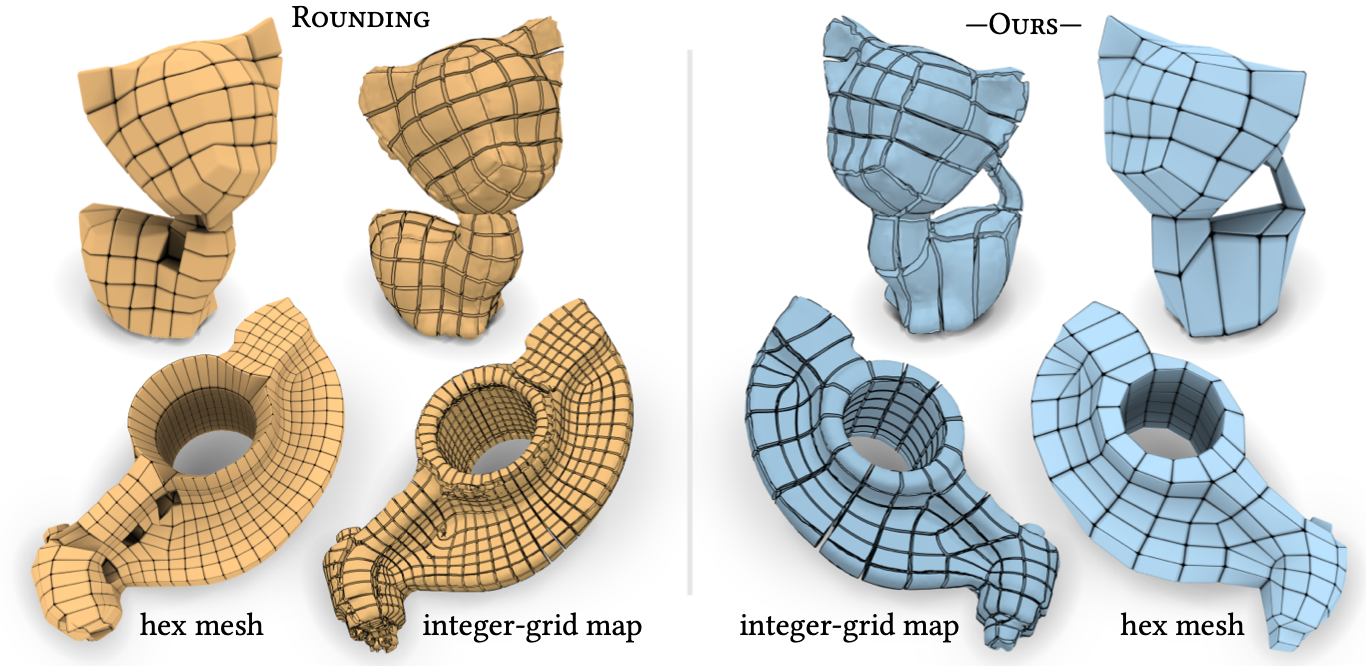
Developments in the field of parametrization-based quad mesh generation on surfaces have been impactful over the past decade. In this context, an important advance has been the replacement of error-prone rounding in the generation of integer-grid maps, by robust quantization methods. In parallel, parametrization-based hex mesh generation for volumes has been advanced. In this volumetric context, however, the state-of-the-art still relies on fragile rounding, not rarely producing defective meshes, especially when targeting a coarse mesh resolution. We present a method to robustly quantize volume parametrizations, i.e., to determine guaranteed valid choices of integers for 3D integer-grid maps. Inspired by the 2D case, we base our construction on a non-conforming cell decomposition of the volume, a 3D analogue of a T-mesh. In particular, we leverage the motorcycle complex, a recent generalization of the motorcycle graph, for this purpose. Integer values are expressed in a differential manner on the edges of this complex, enabling the efficient formulation of the conditions required to strictly prevent forcing the map into degeneration. Applying our method in the context of hexahedral meshing, we demonstrate that hexahedral meshes can be generated with significantly improved flexibility.