 HexHex: Highspeed Extraction of Hexahedral Meshes
HexHex: Highspeed Extraction of Hexahedral Meshes
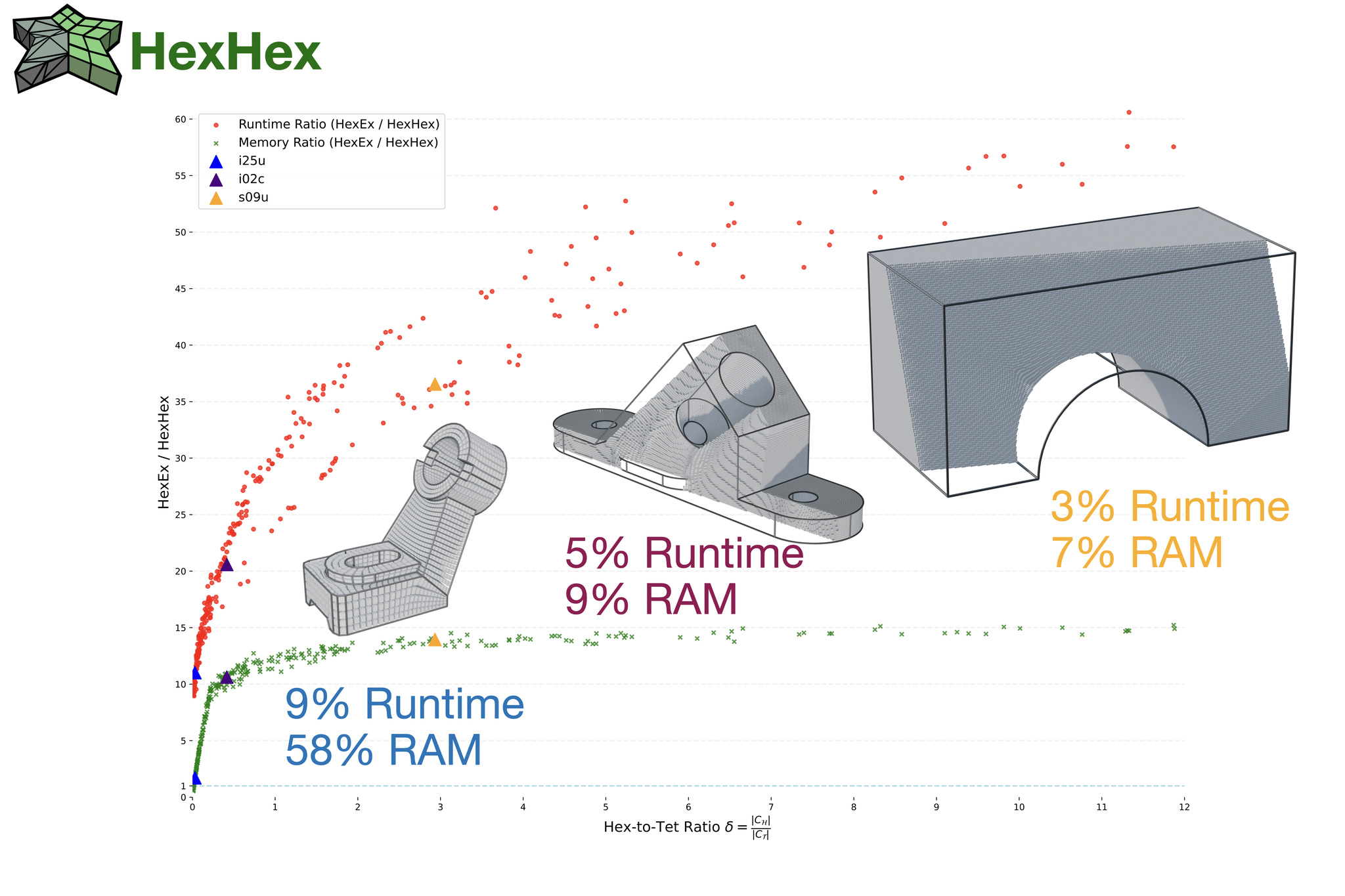
ACM Transactions on Graphics (SIGGRAPH 2025) Modern hexahedral mesh generation relies on integer-grid maps (IGM), which map the Cartesian grid of integer iso-surfaces to a structure-aligned and conforming hexahedral cell complex discretizing the target shape. The hexahedral mesh is formed by iso-surfaces of the map such that an extraction algorithm is needed to convert the implicit map representation into an explicit mesh. State-of-the-art algorithms have been designed with two goals in mind, i.e., (i) unconditional robustness and (ii) tolerance to map defects in the form of inverted or degenerate tetrahedra. Because of significant advancements in the generation of locally injective maps, the tolerance to map defects has become irrelevant. At the same time, there is a growing demand for efficiently handling significantly larger mesh complexities, unfortunately not well served by the state-of-the-art since the tolerance to map defects induces a high runtime cost. Consequently, we present HexHex, a novel (unconditionally robust) hexahedral mesh extraction algorithm for locally injective integer-grid maps designed for maximal performance and scalability. Key contributions include a novel and highly compact mesh data structure based on so-called propellers and a conservative rasterization technique, significantly reducing the number of required exact predicate tests. HexHex not only offers lower asymptotic runtime complexities from a theoretical perspective but also lower constants, enabling in practice a 30x speedup for medium-sized examples and a larger speedup for more complex inputs, specifically when the hex-to-tet ratio is large. We provide a C++ reference implementation, supporting multi-core parallelization and the extraction of curved (piecewise-linear) hexahedral mesh edges and faces, e.g., valuable for subsequent higher-order mesh generation.

|
|
 Quad Mesh Quantization Without a T-Mesh
Quad Mesh Quantization Without a T-Mesh
SGP24: Eurographics Symposium on Geometry Processing Grid preserving maps of triangulated surfaces were introduced for quad meshing because the 2D unit grid in such maps corresponds to a sub-division of the surface into quad-shaped charts. These maps can be obtained by solving a mixed integer optimization problem: Real variables define the geometry of the charts and integer variables define the combinatorial structure of the decomposition. To make this optimization problem tractable, a common strategy is to ignore integer constraints at first, then to enforce them in a so-called quantization step. Actual quantization algorithms exploit the geometric interpretation of integer variables to solve an equivalent problem: They consider that the final quad mesh is a sub-division of a T-mesh embedded in the surface, and optimize the number of sub-divisions for each edge of this T-mesh. We propose to operate on a decimated version of the original surface instead of the T-mesh. It is easier to implement and to adapt to constraints such as free boundaries, complex feature curves network etc.

|
|
 Integer-Sheet-Pump Quantization for Hexahedral Meshing
Integer-Sheet-Pump Quantization for Hexahedral Meshing
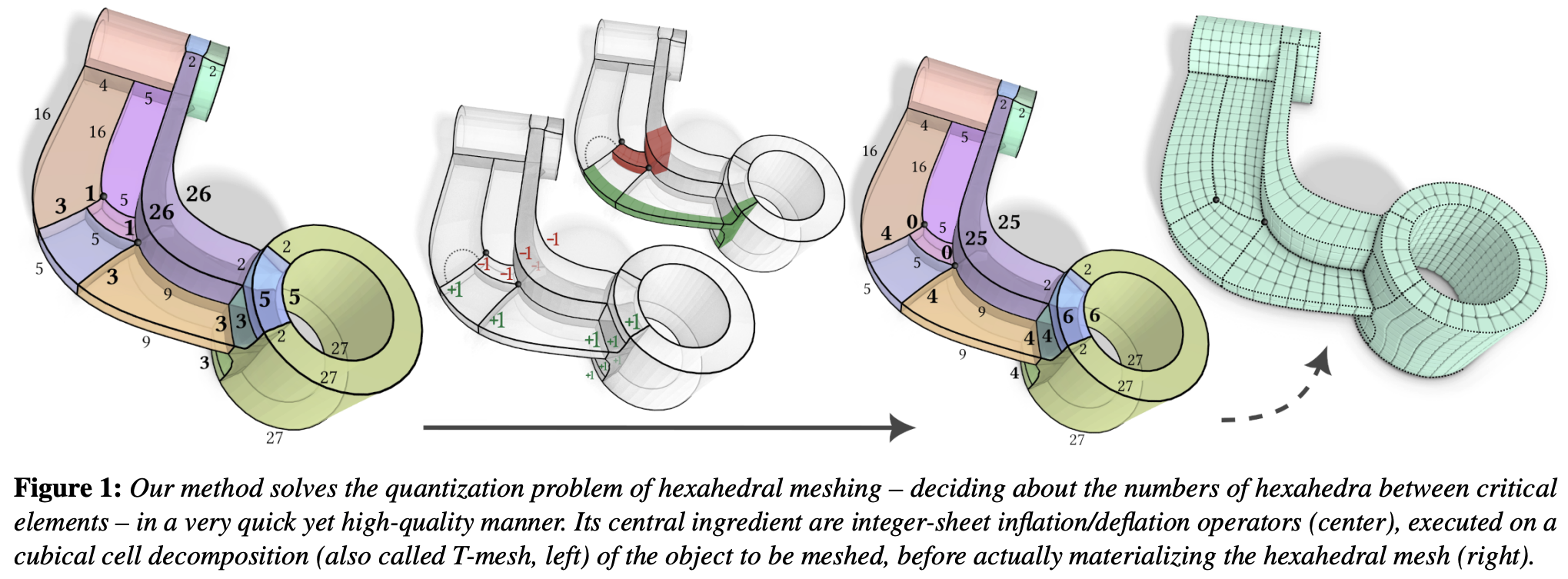
SGP24: Eurographics Symposium on Geometry Processing Several state-of-the-art algorithms for semi-structured hexahedral meshing involve a so called quantization step to decide on the integer DoFs of the meshing problem, corresponding to the number of hexahedral elements to embed into certain regions of the domain. Existing reliable methods for quantization are based on solving a sequence of integer quadratic programs (IQP). Solving these in a timely and predictable manner with general-purpose solvers is a challenge, even more so in the open-source field. We present here an alternative robust and efficient quantization scheme that is instead based on solving a series of continuous linear programs (LP), for which solver availability and efficiency are not an issue. In our formulation, such LPs are used to determine where inflation or deflation of virtual hexahedral sheets are favorable. We compare our method to two implementations of the former IQP formulation (using a commercial and an open-source MIP solver, respectively), finding that (a) the solutions found by our method are near-optimal or optimal in most cases, (b) these solutions are found within a much more predictable time frame, and (c) the state of the art run time is outperformed, in the case of using the open-source solver by orders of magnitude.

|







