State-of-the-art hex meshing algorithms consist of three steps: Frame-field design, parametrization generation, and mesh extraction. However, while the first two steps are usually discussed in detail, the last step is often not well studied. In this paper, we fully concentrate on reliable mesh extraction.

Parametrization methods employ computationally expensive countermeasures to avoid mapping input tetrahedra to degenerate or flipped tetrahedra in the parameter domain because such a parametrization does not define a proper hexahedral mesh. Nevertheless, there is no known technique that can guarantee the complete absence of such artifacts.

We tackle this problem from the other side by developing a mesh extraction algorithm which is extremely robust against typical imperfections in the parametrization. First, a sanitization process cleans up numerical inconsistencies of the parameter values caused by limited precision solvers and floating-point number representation. On the sanitized parametrization, we extract vertices and so-called darts based on intersections of the integer grid with the parametric image of the tetrahedral mesh. The darts are reliably interconnected by tracing within the parametrization and thus define the topology of the hexahedral mesh. In a postprocessing step, we let certain pairs of darts cancel each other, counteracting the effect of flipped regions of the parametrization. With this strategy, our algorithm is able to robustly extract hexahedral meshes from imperfect parametrizations which previously would have been considered defective. The algorithm will be published as an open source library.

The typical goal of surface remeshing consists in finding a mesh that is (1) geometrically faithful to the original geometry, (2) as coarse as possible to obtain a low-complexity representation and (3) free of bad elements that would hamper the desired application. In this paper, we design an algorithm to address all three optimization goals simultaneously. The user specifies desired bounds on approximation error (delta), minimal interior angle (theta) and maximum mesh complexity N (number of vertices). Since such a desired mesh might not even exist, our optimization framework treats only the approximation error bound (delta) as a hard constraint and the other two criteria as optimization goals. More specifically, we iteratively perform carefully prioritized local operators, whenever they do not violate the approximation error bound and improve the mesh otherwise. Our optimization framework greedily searches for the coarsest mesh with minimal interior angle above (theta) and approximation error bounded by (delta). Fast runtime is enabled by a local approximation error estimation, while implicit feature preservation is obtained by specifically designed vertex relocation operators. Experiments show that our approach delivers high-quality meshes with implicitly preserved features and better balances between geometric fidelity, mesh complexity and element quality than the state-of-the-art.

Direction fields and vector fields play an increasingly important role in computer graphics and geometry processing. The synthesis of directional fields on surfaces, or other spatial domains, is a fundamental step in numerous applications, such as mesh generation, deformation, texture mapping, and many more. The wide range of applications resulted in definitions for many types of directional fields: from vector and tensor fields, over line and cross fields, to frame and vector-set fields. Depending on the application at hand, researchers have used various notions of objectives and constraints to synthesize such fields. These notions are defined in terms of fairness, feature alignment, symmetry, or field topology, to mention just a few. To facilitate these objectives, various representations, discretizations, and optimization strategies have been developed. These choices come with varying strengths and weaknesses. This report provides a systematic overview of directional field synthesis for graphics applications, the challenges it poses, and the methods developed in recent years to address these challenges.

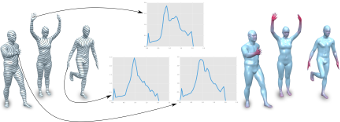
During the last decade a set of surface descriptors have been presented describing local surface features. Recent approaches have shown that augmenting local descriptors with topological information improves the correspondence and segmentation quality. In this paper we build upon the work of Tevs et al. and Sun and Abidi by presenting a surface descriptor which captures both local surface properties and topological features of 3D objects. We present experiments on shape repositories that are provided with ground-truth correspondences (FAUST, SCAPE, TOSCA) which show that this descriptor outperforms current local surface descriptors.