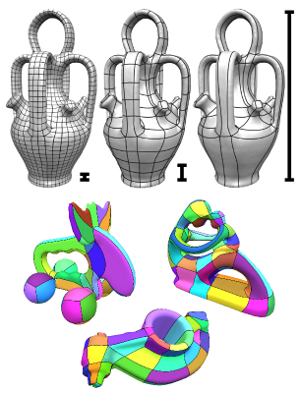
Quadrilateral remeshing approaches based on global parametrization enable many desirable mesh properties. Two of the most important ones are (1) high regularity due to explicit control over irregular vertices and (2) smooth distribution of distortion achieved by convex variational formulations. Apart from these strengths, state-of-the-art techniques suffer from limited reliability on real-world input data, i.e. the determined map might have degeneracies like (local) non-injectivities and consequently often cannot be used directly to generate a quadrilateral mesh. In this paper we propose a novel convex Mixed-Integer Quadratic Programming (MIQP) formulation which ensures by construction that the resulting map is within the class of so called Integer-Grid Maps that are guaranteed to imply a quad mesh. In order to overcome the NP-hardness of MIQP and to be able to remesh typical input geometries in acceptable time we propose two additional problem specific optimizations: a complexity reduction algorithm and singularity separating conditions. While the former decouples the dimension of the MIQP search space from the input complexity of the triangle mesh and thus is able to dramatically speed up the computation without inducing inaccuracies, the latter improves the continuous relaxation, which is crucial for the success of modern MIQP optimizers. Our experiments show that the reliability of the resulting algorithm does not only annihilate the main drawback of parametrization based quad-remeshing but moreover enables the global search for high-quality coarse quad layouts – a difficult task solely tackled by greedy methodologies before.

The most popular and actively researched class of quad remeshing techniques is the family of parametrization based quad meshing methods. They all strive to generate an integer-grid map, i.e. a parametrization of the input surface into R² such that the canonical grid of integer iso-lines forms a quad mesh when mapped back onto the surface in R³. An essential, albeit broadly neglected aspect of these methods is the quad extraction step, i.e. the materialization of an actual quad mesh from the mere “quad texture”. Quad (mesh) extraction is often believed to be a trivial matter but quite the opposite is true: Numerous special cases, ambiguities induced by numerical inaccuracies and limited solver precision, as well as imperfections in the maps produced by most methods (unless costly countermeasures are taken) pose significant challenges to the quad extractor. We present a method to sanitize a provided parametrization such that it becomes numerically consistent even in a limited precision floating point representation. Based on this we are able to provide a comprehensive and sound description of how to perform quad extraction robustly and without the need for any complex tolerance thresholds or disambiguation rules. On top of that we develop a novel strategy to cope with common local fold-overs in the parametrization. This allows our method, dubbed QEx, to generate all-quadrilateral meshes where otherwise holes, non-quad polygons or no output at all would have been produced. We thus enable the practical use of an entire class of maps that was previously considered defective. Since state of the art quad meshing methods spend a significant share of their run time solely to prevent local fold-overs, using our method it is now possible to obtain quad meshes significantly quicker than before. We also provide libQEx, an open source C++ reference implementation of our method and thus significantly lower the bar to enter the field of quad meshing.

The computation of intrinsic, geodesic distances and geodesic paths on surfaces is a fundamental low-level building block in countless Computer Graphics and Geometry Processing applications. This demand led to the development of numerous algorithms – some for the exact, others for the approximative computation, some focussing on speed, others providing strict guarantees. Most of these methods are designed for computing distances according to the standard Riemannian metric induced by the surface’s embedding in Euclidean space. Generalization to other, especially anisotropic, metrics – which more recently gained interest in several application areas – is not rarely hampered by fundamental problems. We explore and discuss possibilities for the generalization and extension of well-known methods to the anisotropic case, evaluate their relative performance in terms of accuracy and speed, and propose a novel algorithm, the Short-Term Vector Dijkstra. This algorithm is strikingly simple to implement and proves to provide practical accuracy at a higher speed than generalized previous methods.

A purely topological approach for the generation of hexahedral meshes from quadrilateral surface meshes of genus zero has been proposed by M. Müller-Hannemann: in a first stage, the input surface mesh is reduced to a single hexahedron by successively eliminating loops from the dual graph of the quad mesh; in the second stage, the hexahedral mesh is constructed by extruding a layer of hexahedra for each dual loop from the first stage in reverse elimination order. In this paper, we introduce several techniques to extend the scope of target shapes of the approach and significantly improve the quality of the generated hexahedral meshes. While the original method can only handle "almost convex" objects and requires mesh surgery and remeshing in case of concave geometry, we propose a method to overcome this issue by introducing the notion of concave dual loops. Furthermore, we analyze and improve the heuristic to determine the elimination order for the dual loops such that the inordinate introduction of interior singular edges, i.e. edges of degree other than four in the hexahedral mesh, can be avoided in many cases.

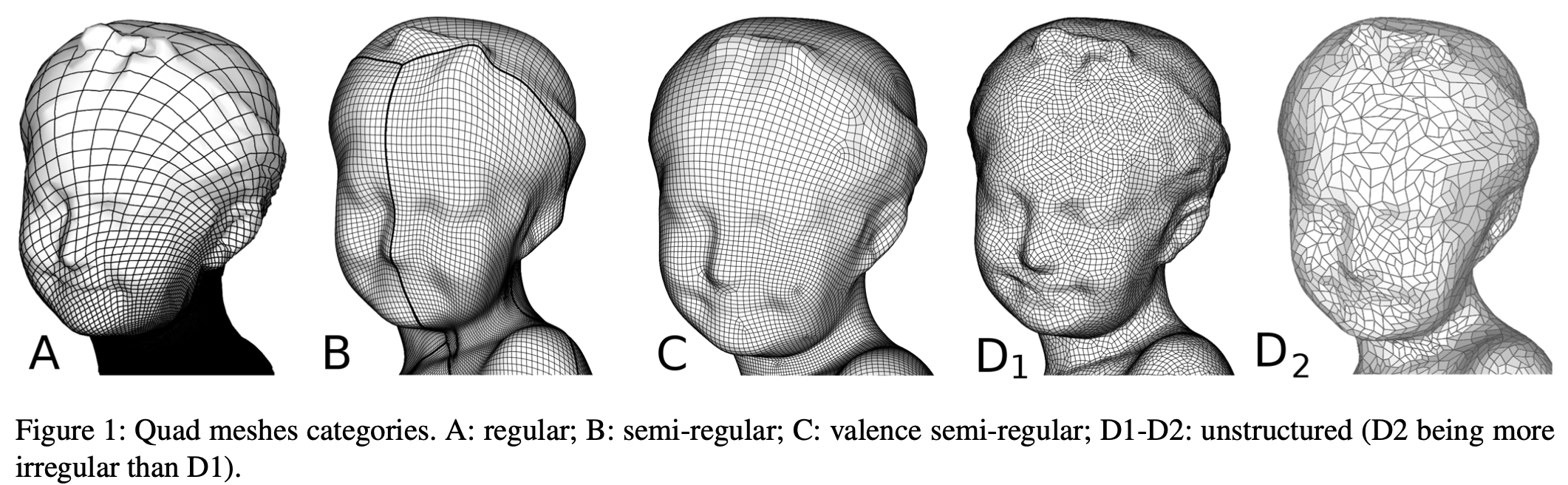
Triangle meshes have been nearly ubiquitous in computer graphics, and a large body of data structures and geometry processing algorithms based on them has been developed in the literature. At the same time, quadrilateral meshes, especially semi-regular ones, have advantages for many applications, and significant progress was made in quadrilateral mesh generation and processing during the last several years. In this survey we discuss the advantages and problems of techniques operating on quadrilateral meshes, including surface analysis and mesh quality, simplification, adaptive refinement, alignment with features, parametrization, and remeshing.