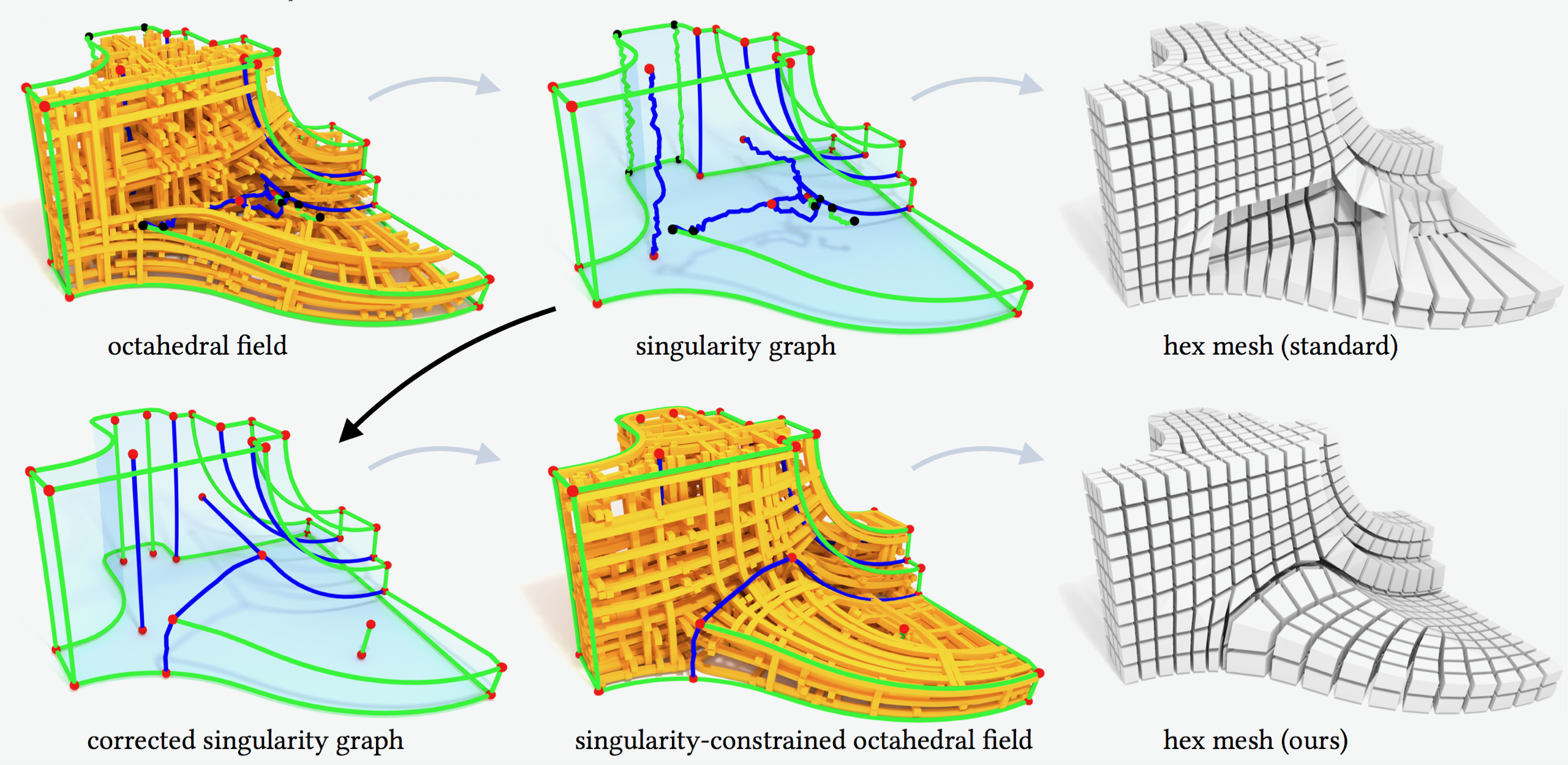
Despite high practical demand, algorithmic hexahedral meshing with guarantees on robustness and quality remains unsolved. A promising direction follows the idea of integer-grid maps, which pull back the Cartesian hexahedral grid formed by integer isoplanes from a parametric domain to a surface-conforming hexahedral mesh of the input object. Since directly optimizing for a high-quality integer-grid map is mathematically challenging, the construction is usually split into two steps: (1) generation of a surface-aligned octahedral field and (2) generation of an integer-grid map that best aligns to the octahedral field. The main robustness issue stems from the fact that smooth octahedral fields frequently exhibit singularity graphs that are not appropriate for hexahedral meshing and induce heavily degenerate integer-grid maps. The first contribution of this work is an enumeration of all local configurations that exist in hex meshes with bounded edge valence, and a generalization of the Hopf-Poincaré formula to octahedral fields, leading to necessary local and global conditions for the hex-meshability of an octahedral field in terms of its singularity graph. The second contribution is a novel algorithm to generate octahedral fields with prescribed hex-meshable singularity graphs, which requires the solution of a large non-linear mixed-integer algebraic system. This algorithm is an important step toward robust automatic hexahedral meshing since it enables the generation of a hex-meshable octahedral field.

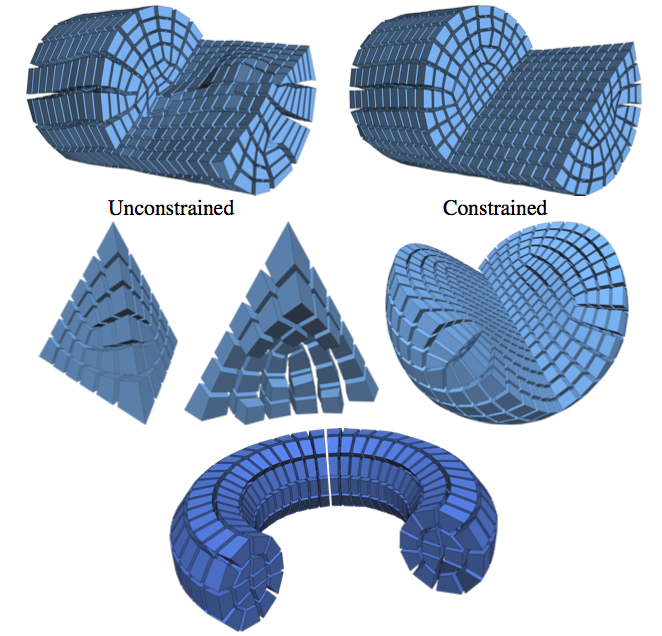
The computation of smooth fields of orthogonal directions within a volume is a critical step in hexahedral mesh generation, used to guide placement of edges and singularities. While this problem shares high-level structure with surface-based frame field problems, critical aspects are lost when extending to volumes, while new structure from the flat Euclidean metric emerges. Taking these considerations into account, this paper presents an algorithm for computing such “octahedral” fields. Unlike existing approaches, our formulation achieves infinite resolution in the interior of the volume via the boundary element method (BEM), continuously assigning frames to points in the interior from only a triangle mesh discretization of the boundary. The end result is an orthogonal direction field that can be sampled anywhere inside the mesh, with smooth variation and singular structure in the interior even with a coarse boundary. We illustrate our computed frames on a number of challenging test geometries. Since the octahedral frame field problem is relatively new, we also contribute a thorough discussion of theoretical and practical challenges unique to this problem.

A new approach to obtain a volumetric discretization from a T-spline surface representation is presented. A T-spline boundary zone is created beneath the surface, while the core of the model is discretized with Lagrangian elements. T-spline enriched elements are used as an interface between isogeometric and Lagrangian finite elements. The thickness of the T-spline zone and thereby the isogeometric volume fraction can be chosen arbitrarily large such that pure Lagrangian and pure isogeometric discretizations are included. The presented approach combines the advantages of isogeometric elements (accuracy and smoothness) and classical finite elements (simplicity and efficiency). Different heat transfer problems are solved with the finite element method using the presented discretization approach with different isogeometric volume fractions. For suitable applications, the approach leads to a substantial accuracy gain.

State-of-the-art hex meshing algorithms consist of three steps: Frame-field design, parametrization generation, and mesh extraction. However, while the first two steps are usually discussed in detail, the last step is often not well studied. In this paper, we fully concentrate on reliable mesh extraction.

Parametrization methods employ computationally expensive countermeasures to avoid mapping input tetrahedra to degenerate or flipped tetrahedra in the parameter domain because such a parametrization does not define a proper hexahedral mesh. Nevertheless, there is no known technique that can guarantee the complete absence of such artifacts.

We tackle this problem from the other side by developing a mesh extraction algorithm which is extremely robust against typical imperfections in the parametrization. First, a sanitization process cleans up numerical inconsistencies of the parameter values caused by limited precision solvers and floating-point number representation. On the sanitized parametrization, we extract vertices and so-called darts based on intersections of the integer grid with the parametric image of the tetrahedral mesh. The darts are reliably interconnected by tracing within the parametrization and thus define the topology of the hexahedral mesh. In a postprocessing step, we let certain pairs of darts cancel each other, counteracting the effect of flipped regions of the parametrization. With this strategy, our algorithm is able to robustly extract hexahedral meshes from imperfect parametrizations which previously would have been considered defective. The algorithm will be published as an open source library.