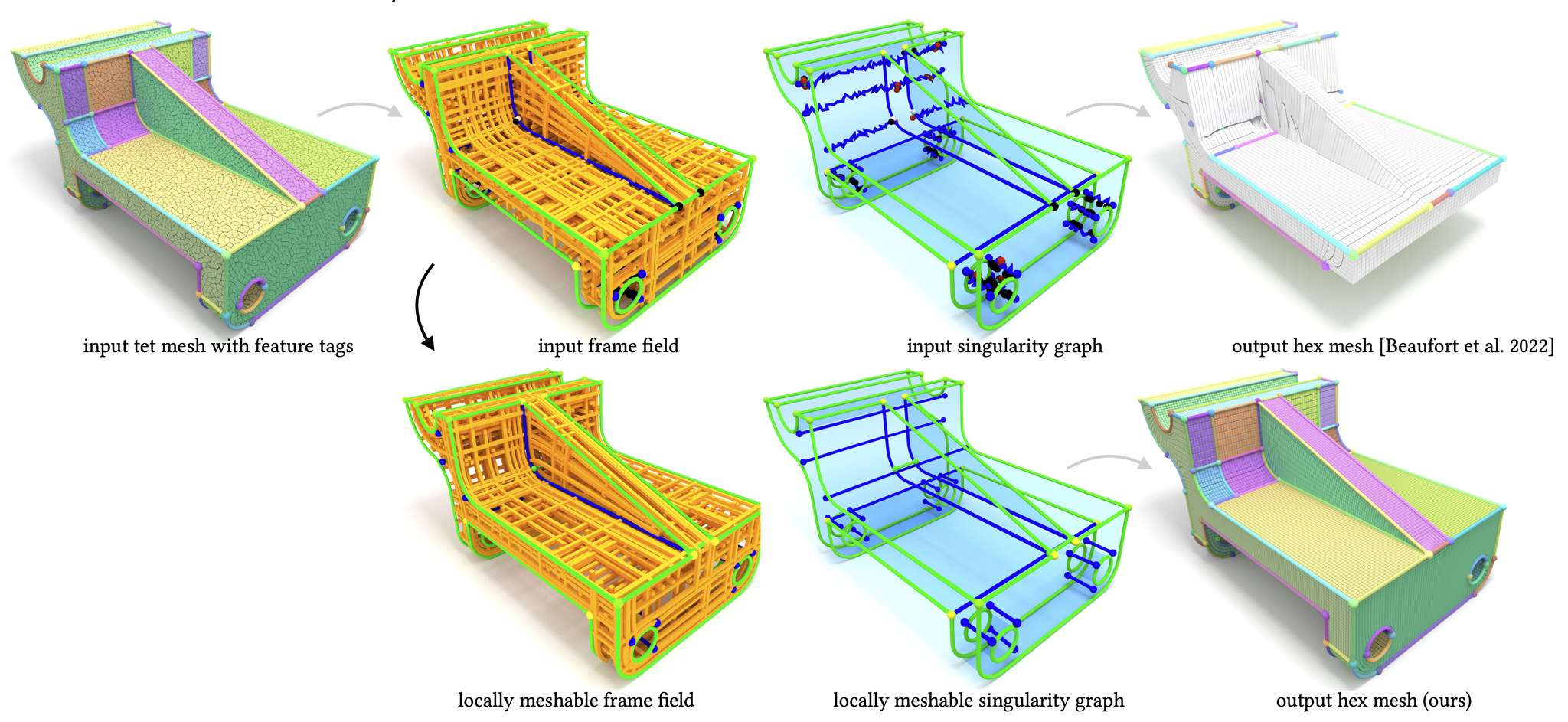
The main robustness issue of state-of-the-art frame field based hexahedral mesh generation algorithms originates from non-meshable topological configurations, which do not admit the construction of an integer-grid map but frequently occur in smooth frame fields. In this article, we investigate the topology of frame fields and derive conditions on their meshability, which are the basis for a novel algorithm to automatically turn a given non-meshable frame field into a similar but locally meshable one. Despite local meshability is only a necessary but not sufficient condition for the stronger requirement of meshability, our algorithm increases the 2% success rate of generating valid integer-grid maps with state-of-the-art methods to 58%, when compared on the challenging HexMe dataset.

HexMe consists of 189 tetrahedral meshes with tagged features and a workflow to generate them. The primary purpose of HexMe meshes is to enable consistent and practically meaningful evaluation of hexahedral meshing algorithms and related techniques, specifically regarding the correct meshing of specified feature points, curves, and surfaces. The tetrahedral meshes have been generated with Gmsh, starting from 63 computer-aided design (CAD) models from various databases. To highlight and label the diverse and challenging aspects of hexahedral mesh generation, the CAD models are classified into three categories: simple, nasty, and industrial. For each CAD model, we provide three kinds of tetrahedral meshes (uniform, curvature-adapted, and box-embedded). The mesh generation pipeline is defined with the help of Snakemake, a modern workflow management system, which allows us to specify a fully automated, extensible, and sustainable workflow. It is possible to download the whole dataset or select individual meshes by browsing the online catalog. The HexMe dataset is built with evolution in mind and prepared for future developments. A public GitHub repository hosts the HexMe workflow, where external contributions and future releases are possible and encouraged. We demonstrate the value of HexMe by exploring the robustness limitations of state-of-the-art frame-field-based hexahedral meshing algorithm. Only for 19 of 189 tagged tetrahedral inputs all feature entities are meshed correctly, while the average success rates are 70.9% / 48.5% / 34.6 % for feature points/curves/surfaces.

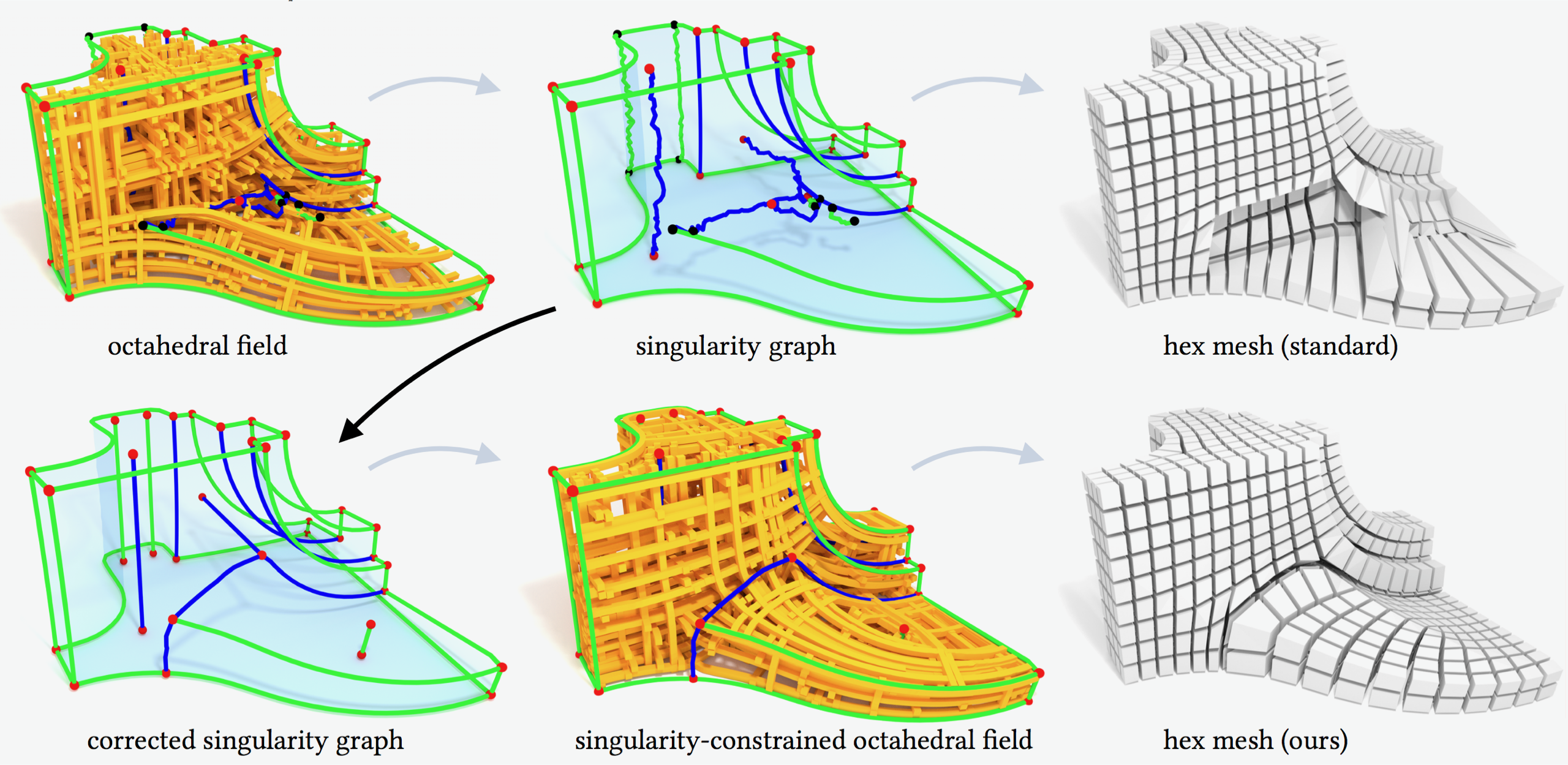
Despite high practical demand, algorithmic hexahedral meshing with guarantees on robustness and quality remains unsolved. A promising direction follows the idea of integer-grid maps, which pull back the Cartesian hexahedral grid formed by integer isoplanes from a parametric domain to a surface-conforming hexahedral mesh of the input object. Since directly optimizing for a high-quality integer-grid map is mathematically challenging, the construction is usually split into two steps: (1) generation of a surface-aligned octahedral field and (2) generation of an integer-grid map that best aligns to the octahedral field. The main robustness issue stems from the fact that smooth octahedral fields frequently exhibit singularity graphs that are not appropriate for hexahedral meshing and induce heavily degenerate integer-grid maps. The first contribution of this work is an enumeration of all local configurations that exist in hex meshes with bounded edge valence, and a generalization of the Hopf-Poincaré formula to octahedral fields, leading to necessary local and global conditions for the hex-meshability of an octahedral field in terms of its singularity graph. The second contribution is a novel algorithm to generate octahedral fields with prescribed hex-meshable singularity graphs, which requires the solution of a large non-linear mixed-integer algebraic system. This algorithm is an important step toward robust automatic hexahedral meshing since it enables the generation of a hex-meshable octahedral field.